数学基础

DeeLMind 数学基础课程

微积分，概率论，统计学，线性代数

导数(Derivative)

• 常见导数

$$\frac{\mathrm{d} C }{\mathrm{d} x} = 0$$

$$\frac{\mathrm{d} x^{u} }{\mathrm{d} x} = ux^{u-1}$$

$$\frac{\mathrm{d} sin(x) }{\mathrm{d} x} = cos(x)$$

$$\frac{\mathrm{d} cos(x) }{\mathrm{d} x} = -sin(x)$$

$$\frac{\mathrm{d} a^{x} }{\mathrm{d} x} = axln(a) (a>0)(a!=1)$$

$$\frac{\mathrm{d} e^{x} }{\mathrm{d} x} = e^{x}$$

• 梯度下降（求min max）

$$f(x) = (x+4)^2 + 1$$

$$\frac{\mathrm{d} f(x) }{\mathrm{d} x}=f(x)^{'} = 2x + 8$$

$$x = x - \theta*\frac{\mathrm{d} f(x) }{\mathrm{d} x}$$

$$x = -3 - \theta * 2$$

$$x = -3 - 0.1 * 2$$

$$x = -3 - 0.2$$

$$x = -3.2 - 0.1 * (-3.2 * 2 + 8) = -3.36$$

偏导(Partial Derivative)

$$f(x,y) = (x+4)^2 + (y+4)^2+ 1$$

$$\frac{\partial f(x,y)}{\partial x} = 2x + 8$$

$$\frac{\partial f(x,y)}{\partial y} = 2y + 8$$

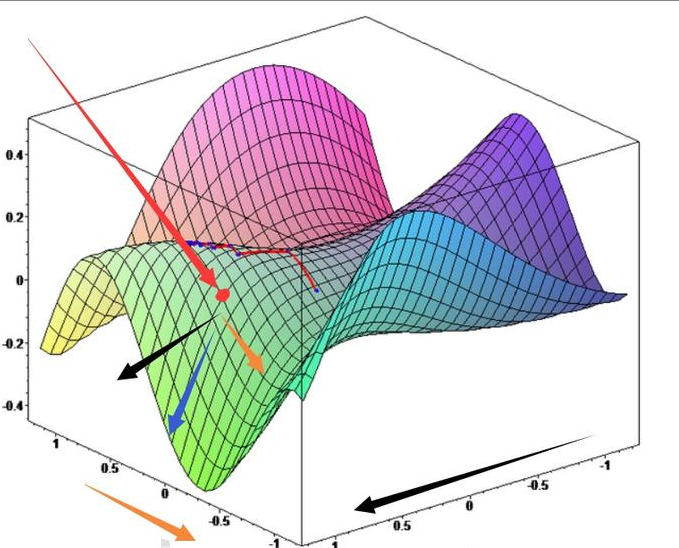
梯度(Dradient)

线性代数

$$\begin{bmatrix} 0 & -1 & 2\end{bmatrix}\begin{bmatrix} -1 \\ 1 \\3\end{bmatrix}$$